| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- 바이낸스
- 선물
- linked list
- 비트코인
- 전위
- 알고리즘
- 오버로딩
- 이진 탐색 트리
- 자료구조
- 연결 리스트
- trading view
- array
- C++
- 트리
- BST
- Basic
- mutable
- 후위
- 숫자
- Python
- Tree
- #선물 #비트코인#알트코인#매매#코인#마진
- 템플릿 함수화
- SCM
- Data Structure
- Windows
- template
- 순회
- 기초
- 문자열
Archives
- Today
- Total
Project Hub
3. 최대공약수, 최소공배수, 소수 본문
728x90
반응형
이전 글
2022.10.11 - [Algorithm/Python] - 2. 피보나치 수열
2. 피보나치 수열
피보나치 수열 피보나치 수(영어: Fibonacci numbers)는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열 피보나치 수열을 두 가지 방법을 이용하여 구현하였다. 1.
projecthub.tistory.com
최대공약수
- 공약수(common divisor)란 두 수 이상의 여러 수의 공통된 약수를 의미
- 최대공약수(GCD)란 두 수 이상의 여러 수의 공약수 중 최대인 수
- 두 수 a, b의 최대공약수는 gcd(a, b) 또는 (a, b)로 나타냄
- 만약 gcd(a, b) = 1이면, 두 수 a, b는 서로소(coprime) 관계
유클리드 호제법(Euclidean algorithm)
2개의 자연수 또는 정식의 최대공약수를 구하는 알고리즘
2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a > b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다.
이 성질에 따라, b를 r로 나눈 나머지 r`를 구하고, 다시 r을 r`로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수다.
a와 b의 최대공약수를 (a, b)라고 하면,
(a, b) = (b, r) = (r, r`) = ... = (last, 0) = last
구현
def find_gcd(first_num, sec_num):
while (sec_num != 0):
result = sec_num
first_num, sec_num = sec_num, first_num % sec_num
return result
def test_find_gcd():
first_num = 78696
sec_num = 19332
print(find_gcd(first_num, sec_num))
if __name__ == "__main__":
test_find_gcd()
최소공배수
- 공배수(common multiple)란 두 수 이상의 여러 수의 공통된 배수를 의미
- 최소공배수(LCM)란 두 수 이상의 여러 수의 공배수 중 최소인 수
- 두 수 a, b의 최소공배수는 lcm(a, b) 또는 [a, b]로 나타냄
- 두 수의 곲을 최대공약수로 나누어 구함
구현
def find_gcd(first_num, sec_num):
while (sec_num != 0):
result = sec_num
first_num, sec_num = sec_num, first_num % sec_num
return result
def least_common_multiple(first_num, sec_num):
return int((first_num * sec_num) / find_gcd(first_num, sec_num))
def test_least_common_multiple():
first_num = 9
sec_num = 6
print(least_common_multiple(first_num, sec_num))
if __name__ == "__main__":
test_least_common_multiple()소수
- 1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수
브루트 포스(brute force)방법으로 구하기 - 무차별 대입 방법
- 소수 여부를 판단하고자 하는 수를 2부터 해당 숫자 전까지 모두 나누어본다.
에라토스테네스의 체(제곱근)를 이용해 구하기
- 소수 구하기의 본질은 약수를 구하는 것이다.
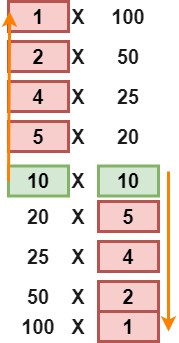
- 가운데 10 x 10을 대칭으로 연산이 반복되고 있다.
- 즉, 10 x 10 이전의 숫자로만 나눗셈을 수행하여 나누어 떨어지지 않으면 소수라고 판단할 수 있는 것이다.
- 따라서 루트 100 을 기준으로 이전 숫자만을 이용해 나눗셈을 진행하여 계산량을 줄이면 된다.
구현
import math
# 브루트 포스 방법
def finding_prime(number):
if number < 4: return True
else:
for i in range(2, number):
if number % i == 0:
return False
return True
# 에라토스테네스의 체 방법
def finding_prime_sqrt(number):
if number < 4: return True
else:
for i in range(2, int(math.sqrt(number)) + 1):
if number % i == 0: return False
return True728x90
반응형
'Algorithm > Python' 카테고리의 다른 글
| 2. 피보나치 수열 (2) | 2022.10.11 |
|---|---|
| 1. 진법 변환 (0) | 2022.10.06 |
Comments


