| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- template
- Windows
- 선물
- Tree
- 오버로딩
- 비트코인
- Basic
- 숫자
- array
- 연결 리스트
- 후위
- #선물 #비트코인#알트코인#매매#코인#마진
- 트리
- 자료구조
- Data Structure
- BST
- C++
- 알고리즘
- SCM
- 바이낸스
- trading view
- 문자열
- Python
- 템플릿 함수화
- 이진 탐색 트리
- 순회
- 기초
- linked list
- mutable
- 전위
Archives
- Today
- Total
Project Hub
1. 진법 변환 본문
728x90
반응형
파이썬 숫자에 대한 개념은 아래의 글을 확인하면 된다.
해당 문제들은 '파이썬 자료구조와 알고리즘' 책에 나오는 내용이다.
2022.10.03 - [Python/기초 개념] - 숫자
숫자
파이썬 자료구조와 알고리즘 책 내용을 정리 1.1 정수 int 로 나타냄. 불변형 (immutable) 정수의 크기는 컴퓨터의 메모리 크기에 의해 제한된다. 적어도 32비트 정수를 나타내는 데 필요한 바이트 수
projecthub.tistory.com
1. 다른 진법의 숫자를 10진수로 변환
- 1001 이라는 숫자가 특정 진법으로 표현된 숫자일 경우, 해당 숫자를 10진법의 숫자로 변환하는 과정은 아래와 같다.
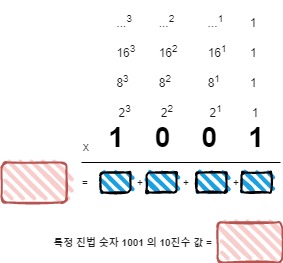
- 위의 그림의 계산 과정에서 맨 오른쪽 자리부터 계산을 하는 과정이 아래의 코드가 된다.
def convert_to_decimal(data, base):
result = 0
multi = 1
while data > 0:
result += data % 10 * multi
multi *= base
data = data // 10
return result
# 굳이 test 함수를 만들어서 호출하지 않아도 될 듯한데.. 스타일인 것 같다.
def test_convert_to_decimal():
data = 1001
base = 2
print(convert_to_decimal(data, base))
if __name__ == "__main__":
test_convert_to_decimal()2. 10진수를 2진법의 숫자로 변환
- 10진수 숫자를 2진법으로 변환하는 방법도 크게 어렵지 않다. 과정은 아래와 같다.

- 10진수를 변환 할 진법으로 나누어간다.
- 나누지 못하는 지점에서 몫과 나머지를 역순으로 붙여서 표기한다.
- 10 이상의 숫자부터는 A(10), B(11), C(12)...로 표현한다.
def convert_from_decimal(data, base):
result = 0
multi = 1
while data > 0:
result += data % base * multi
multi *= 10
data = data // base
return result
def test_convert_from_decimal():
data = 9
base = 2
print(convert_from_decimal(9, 2))
if __name__ == "__main__":
test_convert_from_decimal()3. 10진법 숫자를 20 이하의 진법으로 변환
- 위에 2진법으로의 변환과정과 동일하다.
- 10 이상의 숫자는 문자로 표현해야하기 때문에 문자열을 이용하여 구했다.
def convert_from_decimal_larger_bases(data, base):
# 20진법까지
values = "0123456789ABCDEFGHIJ"
result = ""
while data > 0:
digit = data % base
result = values[digit] + result
data = data // base
return result
def test_convert_from_decimal_larger_bases():
data = 31
base = 16
print(convert_from_decimal_larger_bases(data, base))
if __name__ == "__main__":
test_convert_from_decimal_larger_bases()4. 10진법 숫자를 20 이하의 진법으로 변환을 재귀 방법으로 수행
- 구하는 방법은 동일하고, 다만 과정을 재귀의 방법을 이용하여 구했다.
- 모든 재귀 호출에 대해 재귀 함수는 인수, 반환 주소, 지역 변수를 메모리의 스택에 할당한다.
- 재귀 알고리즘은 최소 O(n)의 시간 복잡도를 가진다.
- 재귀는 계산이 중복되거나 하위 문제가 겹치는 경우 비용이 많이 든다.
- 스택 오버플로가 발생할 수도 있다.
- 재귀에 대해서는 추가로 정리하여 다루도록 하겠다.
def convert_dec_to_any_base_rec(data, base):
values = "0123456789ABCDEFGHIJ"
# 재귀 알고리즘의 base case - 재귀 호출을 유발하지 않는 종료 시나리오
if data < base:
return values[data]
# 자신을 호출
else:
return convert_dec_to_any_base_rec(data // base, base) + values[data % base]
def test_convert_dec_to_any_base_rec():
data = 31
base = 16
print(convert_dec_to_any_base_rec(data, base))
if __name__ == "__main__":
test_convert_dec_to_any_base_rec()
728x90
반응형
'Algorithm > Python' 카테고리의 다른 글
| 3. 최대공약수, 최소공배수, 소수 (0) | 2022.10.11 |
|---|---|
| 2. 피보나치 수열 (2) | 2022.10.11 |
Comments


